FORTH-like languages seemed good for this. Dictating special symbols and punctuation is difficult or impossible, but FORTH can be made to work with just words and numbers. And FORTH is known for building programs up from small definitions, which might be small enough to dictate.
This web page will describe the language as it was in 2014 and as it appeared on github ( https://github.com/strickyak/gerund-lang ). It's in rather rough form and could use a little cleanup and maybe some redesign, but I'm not trying to do that now.
Principal Decisions
After a little experimenting, I arrived at two things:
Gerund is like Joy in many ways: https://www.google.com/search?q=joy+language+concatenative
Compound Words
In practice I often had problems coming up with names for things that I could dictate. I realized that in our ordinary programming languages we frequently compose several things together to create compound words, sometimes with multiple words ("GetVolume", "SetVolume"), sometimes with code letters ("popen", "sprintf"), sometimes numbers ("python3"), sometimes using acronyms ("awk", "grep"), and sometimes just making up words ("foo", "xyzzy").
I arrived at two mechanisms for making compounds:
Ignored Words
All punctuation is deleted and all letters are converted to lowercase before parsing. Also there is a short list of Stop Words that are just ignored: "the", "a", "an", "number", & "also". Inserting these stop words can make sentences easier to say or more easily understood:
"the number 60, the minutes multiplying, also the hours adding" means "60 minutes multiplying hours adding".
REPL
For my REPL (read-eval-print-loop), I would say things to the Google Glass, and it would evaluate the statement and print the result. The Google Glass recognizes a long pause as being the end of one statement, so terminating marks are not needed.
There were only two kinds of statements:
Commands
Commands start with one of these words "define", "list", "definitions", "must" and "test".
Here is what they do:
Expressions and Images
Expressions evaluate and are printed as Python lists. (The interpreter is written in Python, so this is convenient.)
There is one type of result that is special: If the result is a list of lists in which the inner lists contain 9 numbers each, then the result is a picture on a dark background with triangles drawn on it.
Each inner list describes the three corners of a triangle and a color for the triangle, like this:
[ X1 Y1 X2 Y2 X3 Y3 R G B ]
The X,Y coordinates count pixels in the Google Glass's 640 x 360 display, with (0,0) in the lower lefthand corner. The R, G, and B values range 0 to 255.
Here is an example image created from Gerund:
Triangles were actually rendered by a server running this Go code: https://github.com/strickyak/triangle-main
Array Operations
Arithmetic unary and binary operators can be used with lists as well as with scalars, and the results work as in APL:
[ 1 2 2 3 2 ] 10 adding --> [ 11 12 12 13 12 ] [ 1 2 3 ] [ 1 10 100 ] multiplying --> [ 1 20 300 ] [ 1 2 2 3 2 ] 2 equaling --> [ 0 1 1 0 1 ]
You can see that 0 means false and 1 means true. In that example we printed lists in brackets "[" and "]", but in spoken Gerund they would be replaced by the words "opening" and "closing".
Prime Numbers
12 is not prime: http://node1.yak.net:7518/?text=12+priming
13 is prime: http://node1.yak.net:7518/?text=13+priming
The numbers from 1 to 100: http://node1.yak.net:7518/?text=100+counting
The primes from 1 to 100: http://node1.yak.net:7518/?text=100+counting+opening+priming+closing+filtering
How "priming" was defined:
duplicating counting opening getting2 swapping modulo 0 equaling closing mapping summing 2 equaling swapping popping
duplicating ( X -- X X ) duplicates the top of stack.
counting ( N -- [1 2 3... N] ) returns a list of numbers 1 to N
opening & closing create a list quoting everything between opening & closing
getting2 ( X Y -- X Y X ) gets the second thing on the stack
swapping ( X Y -- Y X ) swaps the top two things
modulo ( X Y -- M ) returns X modulo Y as M.
equaling ( X Y -- B ) compares X and Y and returns True or False as B.
mapping ( L F -- R ) applies the quoted list F (like a function) to each element of the list L and returns a list of the results R.
summing ( L -- S ) returns the sum S of the elements in the list L.
popping ( X -- ) pops the top of stack and throws it away.
filtering ( L F -- R ) applies the quoted list F to each element of the list L and returns the elements of L for which the function is true.
Web Demo
http://node1.yak.net:7518/?text=pyramid5
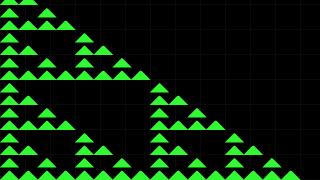
How it works: Alice the Pyramid
http://node1.yak.net:7518/?text=alice
How that worked:
alice9 emits a list of 1 triangle, a seed for the entire construction.
Specifically, alice9 results in this list:
[[0.0, 0.0, 300.0, 300.0, 600.0, 0.0, 44.0, 44.0, 222.0]]That is, the three corners of the triangle are (0,0) (300,300) and (600,0), and the red is 44, green is 44, and blue is 222 (out of 255).
So it is this blue triangle: http://node1.yak.net:7518/?text=alice9
alice8 emits a list of affine functions, which are 6-tuples of: [ mxx mxy myx myy ax ay ] which are 4 matrix elements of M for multiplying times an input point and 2 matrix elements of A for adding to the result.
Specifically, alice8 results in this list:
[[0.5, 0.0, 0.0, 0.5, 0.0, 0.0], [0.5, 0.0, 0.0, 0.5, 0.0, 200.0], [0.5, 0.0, 0.0, 0.5, 300.0, 0.0]]
So you can see that here: http://node1.yak.net:7518/?text=alice8
alice6 is the function to compute the next generation. It's inputs on the stack are a list of input triangles and a list of affine functions. It transforms all input triangles with all functions and produces a new list of triangles (which will be green, regardless of the color of the input triangles).
So if you feed it the seed triangle with "alice9" and the list of affines from "alice8" you will get the next generation which has 3 triangles:
http://node1.yak.net:7518/?text=alice9+alice8+alice6
and you can iterate pushing the affines and computing another generation:
http://node1.yak.net:7518/?text=alice9+alice8+alice6+alice8+alice6
http://node1.yak.net:7518/?text=alice9+alice8+alice6+alice8+alice6+alice8+alice6
More parts of Alice:
alice1 X Y F -> X
takes an X and Y value of a point, and an affine function F, and returns the new X value.
alice2 X Y F -> Y
takes an X and Y value of a point, and an affine function F, and returns the new Y value.
alice3 X Y F -> X Y
takes an X and Y value of a point, and an affine function F, and returns the new X and new Y value.
alice4 T F --> T
takes a triangle T and an affine function F and produces a new triangle, colored green, where each new triangle point is the original triangle point with the affine function applied.
alice5 T FF --> TT
takes a triangle T and a list of affine functions FF and returns a list of triangles TT that result from applying all the functions to that input triangle.
alice6 TT FF --> TT
takes a list of triangles TT and a list of affine functions FF and returns a list of triangles TT, as described above.
Viewing Definitions
To see one definition, use "list" and the word: http://node1.yak.net:7518/?text=list+alice4
To see all definitions, use "definitions": http://node1.yak.net:7518/?text=definitions
To see just the user-defined words, use "list": http://node1.yak.net:7518/?text=list
To find out what the built-in functions are and what they do, read the source! https://github.com/strickyak/gerund-lang/blob/master/gerund.py
Triangle Server
Is the triangle server up? Let's see: