Goal: Compute PI by your favorite method(s).
Monte-Carlo Technique for Estimating Pi:
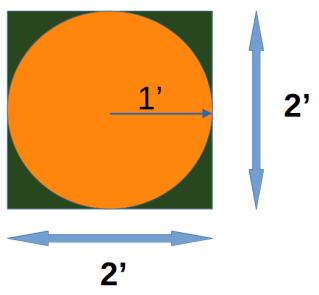
Here's a pizza pie with radius 1 foot inscribed in a pizza box that is 2 foot on a side.
We'll simulate throwing darts at the pizza box to estimate pi.
Area of Pizza Pie = "pi r squared" = 𝜋r² = 𝜋 Area of Pizza Box = 2*2 = 4 Odds of a random dart that hits inside the box also hitting the pie = 𝜋/4
How many darts do you need? The more the better. So let's throw a Petadart: 1.0P🎯 (one quadrillion (1,000,000,000,000,000) darts).
To be able to throw that many, we will need to run many threads in parallel. So we'll use a Map Reduce framework. This will be a special case of Map Reduce in which the reducer is actually a combiner: a binary operator `+` that is both commutative and associative.
Here it is in floating-point Forth (all stack items are 64-bit IEEE floating point numbers):
pi.4th
: map ( map-index-num -- output ) drop rand dup * rand dup * + 1 < ; : combine ( left right -- combined ) + ; : map_combine ( num-maps -- combined ) 0 swap 0 do i map combine loop ; : pi ( num-maps -- ) dup map_combine swap / 4 * . ; 1000000000000000 pi
The input to the mapper is the index number of which map operation it is. That input gets ignored.
The mapper gets two random floating-point numbers between -1.0 and 1.0 (or actually between 0.0 and 1.0 works the same). It squares the random numbers, adds them, and compares that sum to 1.0. If it is less than 1.0, the point is inside the unit circle, so it's like hitting the pizza pie. Greater than 1.0 is a miss.
The mapper outputs 0.0 if it misses, or 1.0 if it hits.
The combiner just sums to floating point numbers.
So the entire map-combine framework will count how many darts hit.
Divide that by how many darts were thrown, and multiply by 4, and you get an approximate to pi.
To run in a distributed computing cluster, we let the little Forth program only compute a Gigadart (one billion (1,000,000,000) darts), and we called that a "big map" in the distributed MR framework. The "big combiner" is still a floating point sum.
So we ran 1,000,000 of these "big maps" on a large cluster of computers and it counted 785398179329381 hits out of 1000000000000000 darts.
4 * 785398179329381 / 1000000000000000.0 = 3.141592717317524
p.s. Where do you get a "floating-point Forth"?
I wrote my own compiler: https://github.com/strickyak/forth-map-combine-pi
compiler.py
import collections import re, sys def PrintIncludes(): print ''' #include <assert.h> #include <stdio.h> #include "runtime.h" ''' def PrintForward(name): print 'extern void Forth_%s(Zorth* p);' % name def PrintStart(name): print '' print 'void Forth_%s(Zorth* p) {' % name def PrintFinish(): print '}' print '' def CompileWord(w): print ' // <<<<< %s >>>>>' % w if re.search('^[-]?[0-9][0-9.]*$', w): print ' p->Push(%s);' % w elif w == 'do': print ' {' print ' double index = p->Pop();' print ' double limit = p->Pop();' print ' do {' elif w == 'loop': print ' index += 1.0;' print ' } while(index < limit);' print ' }' elif w == 'i': print ' p->Push(index);' elif w == '.': print ' printf("%.20g ", p->Pop());' elif w == 'drop': print ' p->Pop();' elif w == 'dup': print ' p->Push(p->Peek());' elif w == 'swap': print ' {double top = p->Peek();' print ' double second = p->PeekN(2);' print ' p->Poke(second); p->PokeN(2, top);}' elif w == 'rot': print ' {double top = p->Peek();' print ' double second = p->PeekN(2);' print ' double third = p->PeekN(3);' print ' p->Poke(third); p->PokeN(2, top); p->PokeN(3, second)}' elif w == 'rand': print ' p->Push(RandomNumber(p->rand_ptr));' elif w == '+': print ' {double top = p->Pop(); p->Poke(p->Peek() + top);}' elif w == '-': print ' {double top = p->Pop(); p->Poke(p->Peek() - top);}' elif w == '*': print ' {double top = p->Pop(); p->Poke(p->Peek() * top);}' elif w == '/': print ' {double top = p->Pop(); p->Poke(p->Peek() / top);}' elif w == '<': print ' {double top = p->Pop(); p->Poke(p->Peek() < top);}' elif w in definitions: print ' Forth_%s(p);' % w else: raise Exception('unknown word: %s' % w) print '' pass definitions = collections.defaultdict(list) def Slurp(): compiling = None ww = sys.stdin.read().split() while ww: w, ww = ww[0], ww[1:] if w == ';': compiling = None elif w == '(': while w != ')': w, ww = ww[0], ww[1:] elif w == ':': compiling, ww = ww[0], ww[1:] elif compiling: definitions[compiling].append(w) else: definitions['program'].append(w) Slurp() print '//', repr(definitions) PrintIncludes() for k in sorted(definitions): PrintForward(k) for k, v in sorted(definitions.items()): PrintStart(k) for w in v: CompileWord(w) PrintFinish()
runtime.h
#include <assert.h> extern double RandomNumber(void*); struct Zorth { explicit Zorth(void* rp) : sp(1), rand_ptr(rp) { CheckEmpty(); } ~Zorth() { CheckEmpty(); } double Pop() { return stack[--sp]; } void Push(double x) { stack[sp++] = x; } double Peek() { return stack[sp-1]; } void Poke(double x) { stack[sp-1] = x; } double PeekN(int n) { return stack[sp-n]; } void PokeN(int n, double x) { stack[sp-n] = x; } void Check() { #if 0 assert(1 <= sp); assert(sp <= SIZE-2); #endif } void CheckEmpty() { #if 0 assert(1 == sp); #endif } inline static constexpr int SIZE = 16; double stack[SIZE]; int sp; void* rand_ptr; }; void Forth_map(Zorth* p); void Forth_combine(Zorth* p); void Forth_map_combine(Zorth* p); double RuntimeMap(Zorth* p, double x); double RuntimeCombine(Zorth* p, double x, double y);
runtime.cc
#include <cstdio> #include <math.h> #include "runtime.h" // The immediate part of the .4th file. extern void Forth_program(Zorth*); double RandomNumber(void* ptr) { return (double)rand() / (double)RAND_MAX; } int main() { Zorth forth(nullptr); Forth_program(&forth); printf("\n"); return 0; }
Makefile
pi : pi.4th runtime.h compiler.py runtime.cc Makefile python compiler.py < pi.4th > pi.cc g++ -O3 -std=c++17 -o pi pi.cc runtime.cc
That program can throw 1,000,000,000 darts in about 16.5 seconds on my laptop.
The "big MR" code is not available.